Shapes of Hermitian matrices and topology of the corresponding isospectral manifolds

Anton Ayzenberg ayzenberga@gmail.com

Algebraic topology, combinatorics, and mathematical physics.

Sochi, SMC, 2023

based on joint works with


V.Buchstaber	V.Cherepanov	M.Masuda	G.Solomadin	K.Sorokin

Graphs and matrix shapes.

$\Gamma$ : a graph with vertex set $[n]=\{1,\ldots,n\}$ and edge set $E_\Gamma$.
$M_n$ : the set of all Hermitian matrices of size $n$.
$A\in M_n$ is called $\Gamma$-shaped if $a_{i,j}=0$ for $\{i,j\}\notin E_\Gamma$.
$M_\Gamma$ : the set of all $\Gamma$-shaped matrices

	$\Rightarrow$	\[ \begin{pmatrix} \ast & \ast & \ast & \ast \\ \ast & \ast & & \\ \ast & & \ast & \\ \ast & & & \ast \end{pmatrix} \]
Star graph		Arrowhead matrix

	$\Rightarrow$	\[ \begin{pmatrix} \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \end{pmatrix} \]
Full graph		Full matrix

	$\Rightarrow$	\[ \begin{pmatrix} \ast & \ast & & \\ \ast & \ast & \ast & \\ & \ast & \ast & \ast \\ & & \ast & \ast \end{pmatrix} \]
Path graph		Tridiagonal matrix

	$\Rightarrow$	\[ \begin{pmatrix} \ast & \ast & & & \ast\\ \ast & \ast & \ast & & \\ & \ast & \ast & \ast & \\ & & \ast & \ast & \ast \\ \ast & & & \ast & \ast \end{pmatrix} \]
Cycle graph		Periodic tridiag- onal matrix

Graphs and matrix shapes.

$\Rightarrow$

\[ \begin{pmatrix} \ast & \ast & & & \ast\\ \ast & \ast & \ast & & \\ & \ast & \ast & \ast & \\ & & \ast & \ast & \ast \\ \ast & & & \ast & \ast \end{pmatrix} \]

$\Rightarrow$

\[ \begin{pmatrix} \ast & \ast & \ast & \ast \\ \ast & \ast & & \\ \ast & & \ast & \\ \ast & & & \ast \end{pmatrix} \]

$\lambda=(\lambda_1<\cdots<\lambda_n)$ : a simple spectrum.
$M_\lambda$ : the set of all matrices with spectrum $\lambda$.
$M_{\Gamma,\lambda}=M_\Gamma\cap M_\lambda$ : the set of all $\Gamma$-shaped matrices with spectrum $\lambda$.
If $\lambda$ is generic, then $M_{\Gamma,\lambda}$ is a smooth closed manifold (follows from Sard's lemma).
$\dim M_{\Gamma,\lambda}=2|E_\Gamma|$.

Torus action on matrices:

Unitary group $U(n)$ acts on $M_n$ by conjugation. It preserves the spectrum.
Let $T\subset U(n)$ be the torus of diagonal matrices. We have induced $T$-action on $M_\lambda$.

This is a torus.
Move cursor to pick an element and act on a matrix!

$\circlearrowright$

*	*	*
*	*	*
*	*	*

[edit]

$T$-action on $M_\lambda$ preserves $\Gamma$-shape for any graph $\Gamma$.
Therefore, the torus $T$ acts on $M_{\Gamma,\lambda}$.

We are interested in toric topology of $M_{\Gamma,\lambda}$

Torus actions. General notions:

$T$ : compact torus.
$T$ acts smoothly (and effectively) on a smooth manifold $X$.
$X^T$ : the set of $T$-fixed points . It is assumed finite and nonempty.

$X_T=X\times_TET$ : Borel construction;
$p\colon X_T\stackrel{X}{\to} BT$ : Serre fibration;
$H^*_T(X)=H^*(X_T)$ : equivariant cohomology module;
$E_2^{p,q}\cong H^p(BT)\otimes H^q(X)\Rightarrow H^{p+q}_T(X)$ : Serre spectral sequence.

Definition: $X$ is called equivariantly formal if its Serre spectral sequence degenerates at $E_2$.

Torus actions. General notions:

$E_2^{p,q}\cong H^p(BT)\otimes H^q(X)\Rightarrow H^{p+q}_T(X)$ : Serre spectral sequence.

Definition: $X$ is called equivariantly formal if its Serre spectral sequence degenerates at $E_2$.

Equivalently (fixed points are isolated): Equivariant formality $\Leftrightarrow$ $H^{odd}(X)=0$.

Problem for today: which manifolds $M_{\Gamma,\lambda}$ are equiavariantly formal?

Examples: full matrices

	$\Rightarrow$	\[ \begin{pmatrix} \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \end{pmatrix} \]
Full graph		Full matrix

Full graph corresponds to the manifold $M_\lambda$ itself.
$U(n)$ acts transitively on $M_\lambda$ with stabilizer $T^n$.
Hence $M_\lambda\cong U(n)/T=Fl_n$, the full flag variety.
It is equivariantly formal.

Examples: tridiagonal

	$\Rightarrow$	\[ \begin{pmatrix} \ast & \ast & & \\ \ast & \ast & \ast & \\ & \ast & \ast & \ast \\ & & \ast & \ast \end{pmatrix} \]
Path graph $\mathbb{I}_n$		Tridiagonal matrix

Path graph corresponds to tridiagonal matrices.
The manifold $M_{\mathbb{I}_n,\lambda}$ was introduced and studied by Tomei'84.
Tomei proved that $M_{\mathbb{I}_n,\lambda}/T$ is a permutohedron.
In modern terminology, $M_{\mathbb{I}_n,\lambda}$ is a quasitoric manifold over permutohedron.
$M_{\mathbb{I}_n,\lambda}$ is equivariantly formal.

Examples: staircase

$\Rightarrow$

\[ \begin{pmatrix} \ast & \ast & \ast & & \\ \ast & \ast & \ast & \ast & \\ \ast & \ast & \ast & \ast & \\ & \ast & \ast & \ast & \ast \\ & & & \ast & \ast \\ \end{pmatrix} \]

Spaces like $M_{\Gamma,\lambda}$ appeared in the literature (de Mari, etc.)
A.-Buchtaber'21 noticed that $M_{\Gamma,\lambda}$ shares many common properties with corresponding regular semisimple Hessenberg varieties. We called them twins.
Using Morse theory, we proved that $M_{\Gamma,\lambda}$ admits even-dimensional cell structure.
Hence $M_{\Gamma,\lambda}$ is equivariantly formal.

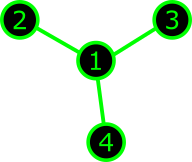
Examples: arrowhead

	$\Rightarrow$	\[ \begin{pmatrix} \ast & \ast & \ast & \ast \\ \ast & \ast & & \\ \ast & & \ast & \\ \ast & & & \ast \end{pmatrix} \]
Star graph $St_n$		Arrowhead matrix

Torus action has complexity $0$. This is a torus manifold.

Theorem (Gal-Januszkiewicz, unpublished): $M_{St_3,\lambda}/T$ is a solid torus with boundary subdivided into hexagons.

Therefore, from Masuda-Panov theorem it follows that
$M_{St_3,\lambda}$ is not equivariantly formal.

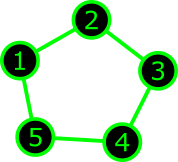
Examples: periodic tridiagonal

	$\Rightarrow$	\[ \begin{pmatrix} \ast & \ast & & & \ast\\ \ast & \ast & \ast & & \\ & \ast & \ast & \ast & \\ & & \ast & \ast & \ast \\ \ast & & & \ast & \ast \end{pmatrix} \]
Cycle graph $Cy_n$		Periodic tridiag- onal matrix

Torus action of complexity $1$ in general position.

A.'20: $M_{Cy_n,\lambda}$ is not equivariantly formal for $n\geqslant 4$.

$\pi_1(M_{Cy_n,\lambda})\cong \mathbb{Z}^{n-3}$ (if $M_{Cy_n,\lambda}$ is smooth).

A.-Masuda'19: If there is an equivariantly formal torus action of complexity $1$ in general position on $X$, then $X/T$ is a homology sphere.

But I proved: $M_{Cy_n,\lambda}/T\cong S^4\times T^{n-3}$.

Indifference graphs:

Which graphs correspond to staircase matrices?

Definition: Graph $\Gamma$ is called indifference graph if it is the intersection graph of some collection of unit intervals on a line $\mathbb{R}$.

Also called unit interval graphs or proper interval graphs.

Theorem (Mertzios'08): $\Gamma$ represents staircase matrices $\Leftrightarrow$ $\Gamma$ is an indifference graph.

$\Rightarrow$

\[ \begin{pmatrix} \ast & \ast & \ast & & \\ \ast & \ast & \ast & \ast & \\ \ast & \ast & \ast & \ast & \\ & \ast & \ast & \ast & \ast \\ & & & \ast & \ast \\ \end{pmatrix} \]

Warning:

Some matrices are staircase even if they don't look so:

$\Rightarrow$

\[ \begin{pmatrix} \ast & \ast & \ast \\ \ast & \ast & \\ \ast & & \ast \end{pmatrix} \]

$\Rightarrow$

\[ \begin{pmatrix} \ast & \ast & \\ \ast & \ast & \ast \\ & \ast & \ast \end{pmatrix} \]

Spaces $M_{\Gamma,\lambda}$ in these two cases are homeomorphic. The space depends only on a graph.

Result

For any graph $\Gamma$ on $n$ vertices we have:

$T$-action on $M_{\Gamma,\lambda}$ has $n!$ many fixed points,
therefore $\beta_{even}-\beta_{odd}=\chi(M_{\Gamma,\lambda})=n!$,
therefore $\beta(M_{\Gamma,\lambda})\geqslant n!$.

Theorem: The following conditions are equivalent:

$\Gamma$ is an indifference graph,

$M_{\Gamma,\lambda}$ is equivariantly formal;

$\beta(M_{\Gamma,\lambda})=n!$.

Topological complexity

Corollary: If $\Gamma$ is not indifference, then

$\beta(M_{\Gamma,\lambda})>n!$, hence

any Morse-Smale flow on $M_{\Gamma,\lambda}$ has $>n!$ stationary points.

This gives an applied math intuition behind this result.

QR-algorithm

Original matrix:


0
0	0
0	0	0

At each step we represent a matrix $A_i$ as $Q\cdot R$ and take $A_{i+1}=R\cdot Q$. Here $Q$ is orgthogonal, $R$ is upper triangular.

Fill in the matrix above.
Press "u" to upload.
Press "q" to make QR step.

After 0 iterations:

*	*	*	*
*	*	*	*
*	*	*	*
*	*	*	*

QR-algorithm

QR-algorithm preserves spectrum and symmetricity.
It has $n!$ limit points (diagonal matrices with spectrum at the diagonal).
It is a Morse-Smale cascade on $M_\lambda$.
QR-algorithm preserves staircase shape.
It is a flow on $M_{\Gamma,\lambda}$ for indifference graph $\Gamma$.

Toda flow

Continuous version of QR-algorithm.
Same properties.
Honest gradient flow of a Morse function.

How we prove:

We need to prove

"$\Gamma$ is not an indifference graph" $\Rightarrow$ "$M_{\Gamma,\lambda}$ is not formal".

Lemma: If $M_{\Gamma,\lambda}$ is formal and $\Gamma'$ is an induced subgraph of $\Gamma$, then $M_{\Gamma',\lambda}$ is also formal.


Induced	Not induced

Conclusion: we only need to prove non-formality for "minimal" non-indifference graphs.

How we prove:

Theorem (Roberts'70): $\Gamma$ is not an indifference graph $\Leftrightarrow$ it has one of the following induced subgraphs:


Claw $St_3$	Holes $Cy_k$, $k\geq 4$	$Net$	$Sun$

Conclusion: we only need to prove non-formality for this list of forbidden graphs.

Claw $St_3$ and Holes $Cy_n$ ($n\geqslant 4$) are already studied: non-formality of $M_{\Gamma,\lambda}$ is proved.
It remains to prove non-formality for $Net$ and $Sun$.

To do this, we developed a general approach.

Face submanifolds:

Let $H\subseteq T$ be a connected subgroup.

Definition:

A connected component of the fixed point manifold $X^H$ is called an invariant submanifold.
If an invariant submanifold intersects $X^T$, it is called a face submanifold.

The rank of an invariant (face) submanifold $Y$ is the dimension of generic toric orbit on $Y$.
Face submanifolds are partially ordered by inclusion.

Fixed points = face submanifolds of rank $0$.
The greatest face submanifold is $X$ itself. It has rank $\dim T$.

Definition: The poset of all face submanifolds is denoted $S(X)$. It is graded by ranks.

Face poset and formality

$S(X)_r$ : the $r$-skeleton, the poset of all face submanifolds of rank $\leqslant r$.

We say a $T$-action has GKM type if every face submanifold of rank $1$ is a $2$-sphere.
Every $M_{\Gamma,\lambda}$ has GKM type.

Let $|S|$ denote the geometrical realization of a poset $S$.

Theorem (A.-Masuda-Solomadin'22):

Assume an $T$-action on $X$ is equivariantly formal and $\dim T\geqslant 4$. Then for any $r\geqslant 4$ we have \[ \tilde{H}^i(|S(X)_r|)=0 \quad\text{ for }\quad i\leq 3. \] In other words, the skeleton $|S(X)_r|$ is $3$-acyclic.

Cases:


$Net$	$Sun$

\[ \begin{pmatrix} \ast & \ast & \ast & \ast & & \\ \ast & \ast & \ast & & \ast & \\ \ast & \ast & \ast & & & \ast \\ \ast & & & \ast & & \\ & \ast & & & \ast & \\ & & \ast & & & \ast \\ \end{pmatrix}, \begin{pmatrix} \ast & \ast & \ast & & \ast & \ast \\ \ast & \ast & \ast & \ast & & \ast\\ \ast & \ast & \ast & \ast & \ast & \\ & \ast & \ast & \ast & & \\ \ast& & \ast & & \ast & \\ \ast & \ast & & & & \ast \\ \end{pmatrix} \]

$M_{Net,\lambda}$ is $12$-dim manifold with $5$-dim torus action.

$M_{Sun,\lambda}$ is $18$-dim with $5$-dim torus action.

It is impossible to compute $H^{odd}$ of these spaces...

...however, we can describe the poset $S(M_{\Gamma,\lambda})$ and compute its homology in low degrees.

So we did the following:

A.-Buchstaber'22: Described the poset $S(M_{\Gamma,\lambda})$. It is isomorphic to the core of the graphicahedron of $\Gamma$.

Assumption $M_{Net,\lambda}$ and $M_{Sun,\lambda}$ are formal, implies $|S(M_{Net,\lambda})_4|$ and $|S(M_{Sun,\lambda})_4|$ are 3-acyclic.
So we tried to check, whether this is true.

Cases:


$Net$	$Sun$

We unpacked our computers, ran Sage, and calculated:

Theorem (A.-Sorokin'22): $|S(M_{Net,\lambda})_4|$ and $|S(M_{Sun,\lambda})_4|$ are 2-acyclic. But $\beta_3(|S(M_{Net,\lambda})_4|)=5$ and $\beta_3(|S(M_{Sun,\lambda})_4|)=5$. *Coefficients in $\mathbb{Z}_2$.

Since face posets are not $3$-acyclic, manifolds are not equivariantly formal.

This finalizes the proof of the main theorem.

Thank you for your attention!

Our papers related to this work:

A.A.Ayzenberg, V.M.Buchstaber, Manifolds of isospectral arrow matrices, Sbornik: Mathematics 212:5 (2021), 3-36. [link]
A.A.Ayzenberg, V.M.Buchstaber, Manifolds of isospectral matrices and Hessenberg varieties, IMRN 2021:21 (2021), 16671-16692. [link]
A.Ayzenberg, Space of isospectral periodic tridiagonal matrices, Alg. and Geom. Topology 20 (2020), 2957-2994. [link]
A.Ayzenberg, M.Masuda, Orbit spaces of equivariantly formal torus actions, Transformation Groups, 2023, preprint. [link]
A.Ayzenberg, V.Cherepanov, Matroids in toric topology, 2022, [preprint].
A.Ayzenberg, M.Masuda, G.Solomadin, How is a graph not like a manifold?, to appear in Sbornik: Mathematics [link].
A.Ayzenberg, V.Buchstaber, Cluster-permutohedra and submanifolds of flag varieties with torus actions, IMRN 2023 [link].
A.Ayzenberg, K.Sorokin, Topological approach to diagonalization algorithms, 2022, preprint. [preprint].

Technical reference:

An extended version of this presentation is available here.

Source code and instructions on usage lie on Github.